=> Bất đẳng thức đúng với r=k+1.
Bách khoa toàn thư mở Wikipedia
Bài này viết về bất đẳng thức trong phép nhân vectơ. Đối với bài về bất đẳng thức trung bình cộng và trung bình nhân, xem
Bất đẳng thức Cauchy.
Trong
toán học,
bất đẳng thức Cauchy–Schwarz , còn được gọi là
bất đẳng thức Schwarz ,
bất đẳng thức Cauchy , hoặc bằng cái tên khá dài là
bất đẳng thức Cauchy–Bunyakovski–Schwarz, đặt theo tên của
Augustin Louis Cauchy,
Viktor Yakovlevich Bunyakovskyvà
Hermann Amandus Schwarz, là một bất đẳng thức thường được áp dụng trong nhiều lĩnh vực khác nhau của toán học, chẳng hạn trong
đại số tuyến tính dùng cho các
vector, trong
giải tích dùng cho các
chuỗi vô hạn và
tích phân của các tích, trong
lý thuyết xác suất dùng cho các
phương sai và
hiệp phương sai. Tài liệu giáo khoa Việt Nam gọi bất đẳng thức này là
bất đẳng thức Bunyakovski hoặc bằng tên dài nói trên nhưng đảo thứ tự là
bất đẳng thức Bunyakovski–Cauchy-Schwarz nên thường viết tắt là
bất đẳng thức BCS. Cũng cần tránh nhầm lẫn với
bất đẳng thức trung bình cộng và trung bình nhân mà tài liệu giáo khoa tại Việt Nam gọi là bất đẳng thức Cauchy.

Như vậy, có vẻ như bất đẳng thức này cho thấy có mối liên quan giữa khái niệm "góc của hai vector" với khái niệm tích trong, mặc dầu các khái niệm của hình học Euclide có thể không còn mang đầy đủ ý nghĩa trong trường hợp này, và ở mức độ nào đấy, nó cho thấy ý niệm các không gian tích trong là một sự tổng quát hoá của không gian Euclide.
Một hệ quả quan trọng của bất đẳng thức Cauchy-Schwarz: tích trong là một
hàm liên tục.
Một dạng khác của bất đẳng thức Cauchy-Schwarz được phát biểu dưới đây bằng cách dùng ký hiệu
chuẩn, với chuẩn ở đây được hiểu là chuẩn trên không gian tích trong
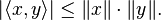
Năm 1821, Cauchy chứng minh bất đẳng thức này trong trường hợp các vector thực và hữu hạn chiều và đến năm 1859, học trò của Cauchy là V.Ya. Bunyakovsky nhận xét rằng khi chúng ta lấy
giới hạn chúng ta có thể thu được dạng tích phân của bất đẳng thức này. Kết quả tổng quát trong trường hợp không gian tích trong được chứng minh bởi K.H.A. Schwarz vào năm 1885.
Chứng minh
Bất đẳng thức này rõ ràng đúng với
y = 0, vì thế ta có thể giả sử <
y,
y> khác zero. Giả sử
λ là một
số phức bất kỳ. Khi đó, chúng ta có bất đẳng thức chắc chắn đúng như sau:
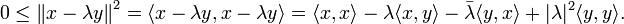
Chọn

chúng ta được

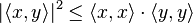
hay tương đương:

(điều phải chứng minh)
Một số trường hợp đặc biệt đáng chú ý
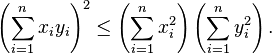 . Đặc biệt hơn, trong không gian Euclide với số chiều bằng 2 hay 3, nếu tích vô hướngđược xác định theo góc giữa hai vector, khi đó bất đẳng thức này trở thành một bất đẳng thức dễ dàng chứng minh:
. Đặc biệt hơn, trong không gian Euclide với số chiều bằng 2 hay 3, nếu tích vô hướngđược xác định theo góc giữa hai vector, khi đó bất đẳng thức này trở thành một bất đẳng thức dễ dàng chứng minh:  . Hơn nữa, trong trường hợp này, bất đẳng thức Cauchy-Schwarz có thể suy ra từ đồng nhất thức Lagrange bằng cách bỏ qua một số hạng. Trong trường hợp số chiều n = 3, đồng nhất thức Lagrange có dạng:
. Hơn nữa, trong trường hợp này, bất đẳng thức Cauchy-Schwarz có thể suy ra từ đồng nhất thức Lagrange bằng cách bỏ qua một số hạng. Trong trường hợp số chiều n = 3, đồng nhất thức Lagrange có dạng:
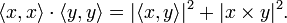
Hệ quả của bất đẳng thức này là bất đẳng thức

Một hệ quả khác, đó là bất đẳng thức Schwarz hay cũng được nhiều tài liệu gọi là bất đẳng thức Cauchy Schwarz

Một vài ứng dụng
Bất đẳng thức tam giác cho tích trong thường được xem là một hệ quả của bất đẳng thức Cauchy-Schwarz như sau: cho các vector
x và
y,
-
Lấy căn bậc hai hai vế ta được bất đẳng thức tam giác.
Bất đẳng thức Cauchy-Schwarz thường được dùng để chứng minh
Xem thêm
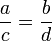

 với quy ước nếu một số bi nào đó (i = 1, 2, 3,..., n) bằng 0 thì ai tương ứng bằng 0.
với quy ước nếu một số bi nào đó (i = 1, 2, 3,..., n) bằng 0 thì ai tương ứng bằng 0. tức là
tức là  mà rõ ràng đúng.Bây giờ giả sử bất đẳng thức đúng với r=k:
mà rõ ràng đúng.Bây giờ giả sử bất đẳng thức đúng với r=k: Cần chứng minh:
Cần chứng minh: Thật vậy,
Thật vậy,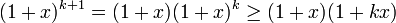 (vì theo giả thiết
(vì theo giả thiết  )
)  (vì
(vì  )=> Bất đẳng thức đúng với r=k+1.Theo nguyên lý quy nạp, chúng ta suy ra bất đẳng thức đúng với mọi
)=> Bất đẳng thức đúng với r=k+1.Theo nguyên lý quy nạp, chúng ta suy ra bất đẳng thức đúng với mọi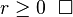 Số mũ r có thể tổng quát hoá thành số thực bất kỳ như sau: nếu x > −1, thìvới r ≤ 0 or r ≥ 1, vàvới 0 ≤ r ≤ 1.Có thể chứng minh bất đẳng thức tổng quát hoá nói trên bằng cách so sánh các đạo hàm.Một lần nữa, bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt nếu x ≥ -1 và 1 ≤ r thuộc tập số tự nhiên.
Số mũ r có thể tổng quát hoá thành số thực bất kỳ như sau: nếu x > −1, thìvới r ≤ 0 or r ≥ 1, vàvới 0 ≤ r ≤ 1.Có thể chứng minh bất đẳng thức tổng quát hoá nói trên bằng cách so sánh các đạo hàm.Một lần nữa, bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt nếu x ≥ -1 và 1 ≤ r thuộc tập số tự nhiên.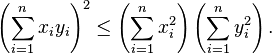 . Đặc biệt hơn, trong không gian Euclide với số chiều bằng 2 hay 3, nếu tích vô hướngđược xác định theo góc giữa hai vector, khi đó bất đẳng thức này trở thành một bất đẳng thức dễ dàng chứng minh:
. Đặc biệt hơn, trong không gian Euclide với số chiều bằng 2 hay 3, nếu tích vô hướngđược xác định theo góc giữa hai vector, khi đó bất đẳng thức này trở thành một bất đẳng thức dễ dàng chứng minh:  . Hơn nữa, trong trường hợp này, bất đẳng thức Cauchy-Schwarz có thể suy ra từ đồng nhất thức Lagrange bằng cách bỏ qua một số hạng. Trong trường hợp số chiều n = 3, đồng nhất thức Lagrange có dạng:
. Hơn nữa, trong trường hợp này, bất đẳng thức Cauchy-Schwarz có thể suy ra từ đồng nhất thức Lagrange bằng cách bỏ qua một số hạng. Trong trường hợp số chiều n = 3, đồng nhất thức Lagrange có dạng:

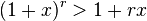



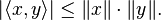
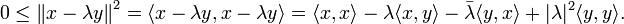


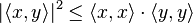

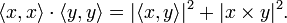







Không có nhận xét nào:
Đăng nhận xét